Основные виды сортировок и примеры их реализации
На собеседованиях будущим стажёрам-разработчикам дают задания на знание структур данных и алгоритмов — в том числе сортировок. Академия Яндекса и соавтор специализации «Искусство разработки на современном C++» Илья Шишков составили список для подготовки с методами сортировки, примерами их реализации и гифками, чтобы лучше понять, как они работают.
Пузырьковая сортировка и её улучшения
Сортировка пузырьком
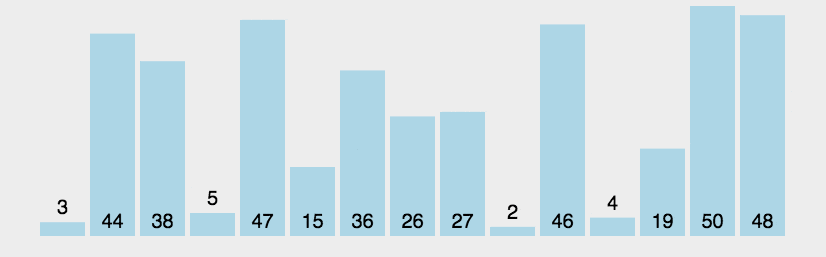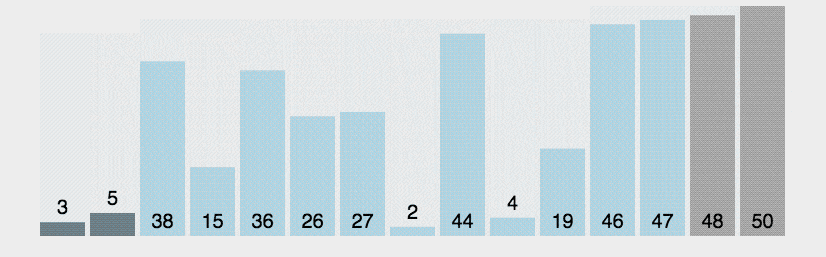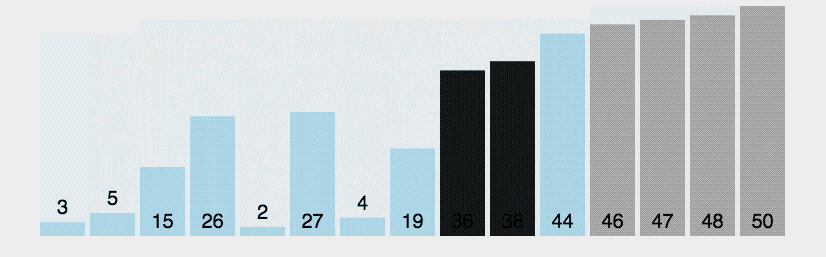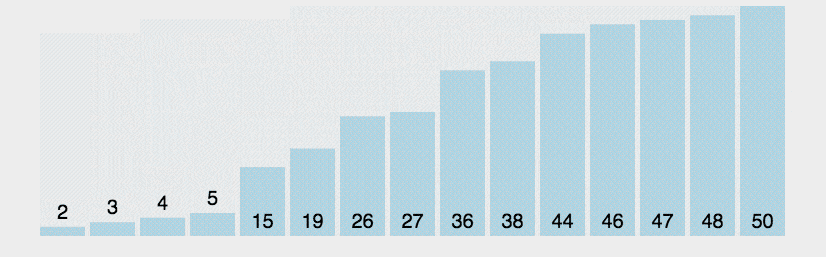
Сортировка пузырьком — один из самых известных алгоритмов сортировки. Здесь нужно последовательно сравнивать значения соседних элементов и менять числа местами, если предыдущее оказывается больше последующего. Таким образом элементы с большими значениями оказываются в конце списка, а с меньшими остаются в начале.
Этот алгоритм считается учебным и почти не применяется на практике из-за низкой эффективности: он медленно работает на тестах, в которых маленькие элементы (их называют «черепахами») стоят в конце массива. Однако на нём основаны многие другие методы, например, шейкерная сортировка и сортировка расчёской.

Сортировка перемешиванием (шейкерная сортировка)
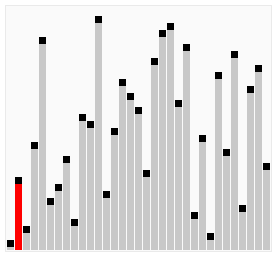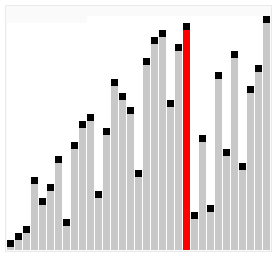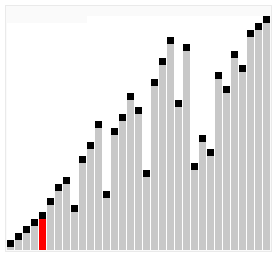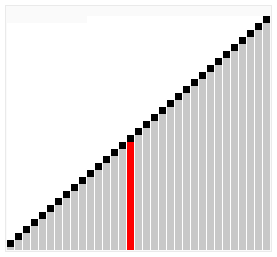
Шейкерная сортировка отличается от пузырьковой тем, что она двунаправленная: алгоритм перемещается не строго слева направо, а сначала слева направо, затем справа налево.

Сортировка расчёской
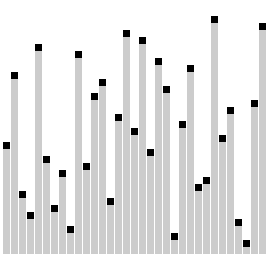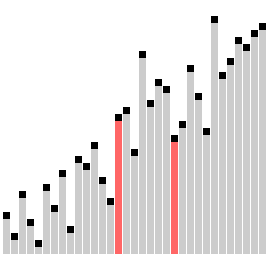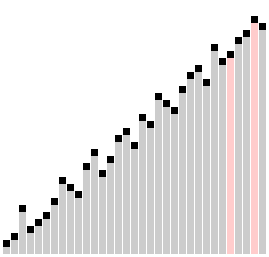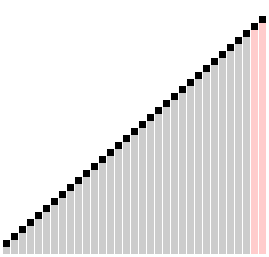
Сортировка расчёской — улучшение сортировки пузырьком. Её идея состоит в том, чтобы «устранить» элементы с небольшими значения в конце массива, которые замедляют работу алгоритма. Если при пузырьковой и шейкерной сортировках при переборе массива сравниваются соседние элементы, то при «расчёсывании» сначала берётся достаточно большое расстояние между сравниваемыми значениями, а потом оно сужается вплоть до минимального.
Первоначальный разрыв нужно выбирать не случайным образом, а с учётом специальной величины — фактора уменьшения, оптимальное значение которого равно 1,247. Сначала расстояние между элементами будет равняться размеру массива, поделённому на 1,247; на каждом последующем шаге расстояние будет снова делиться на фактор уменьшения — и так до окончания работы алгоритма.

Простые сортировки
Сортировка вставками
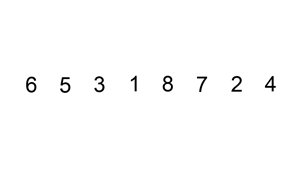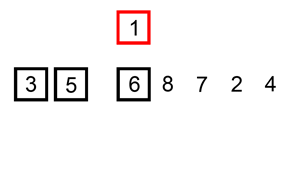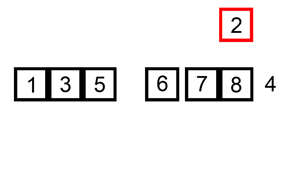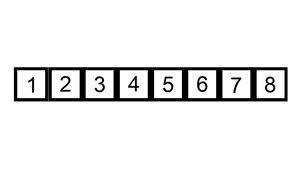
При сортировке вставками массив постепенно перебирается слева направо. При этом каждый последующий элемент размещается так, чтобы он оказался между ближайшими элементами с минимальным и максимальным значением.

Сортировка выбором
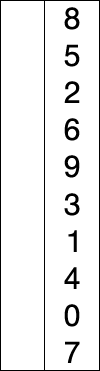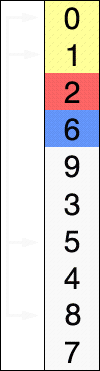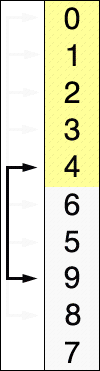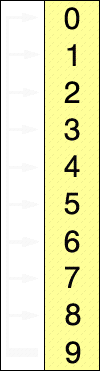
Сначала нужно рассмотреть подмножество массива и найти в нём максимум (или минимум). Затем выбранное значение меняют местами со значением первого неотсортированного элемента. Этот шаг нужно повторять до тех пор, пока в массиве не закончатся неотсортированные подмассивы.

Эффективные сортировки
Быстрая сортировка
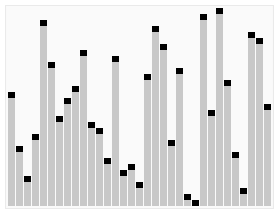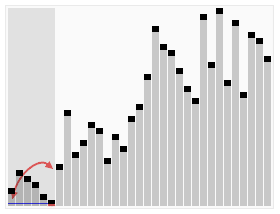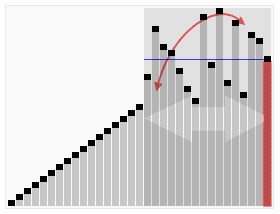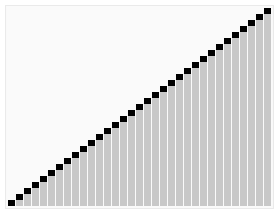
Этот алгоритм состоит из трёх шагов. Сначала из массива нужно выбрать один элемент — его обычно называют опорным. Затем другие элементы в массиве перераспределяют так, чтобы элементы меньше опорного оказались до него, а большие или равные — после. А дальше рекурсивно применяют первые два шага к подмассивам справа и слева от опорного значения.
Быструю сортировку изобрели в 1960 году для машинного перевода: тогда словари хранились на магнитных лентах, а сортировка слов обрабатываемого текста позволяла получить переводы за один прогон ленты, без перемотки назад.

Сортировка слиянием
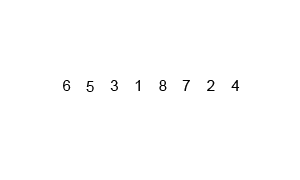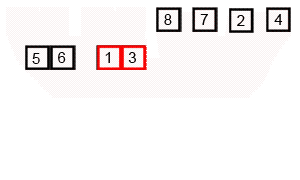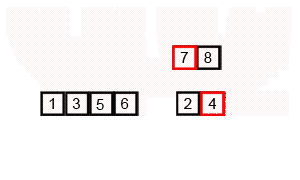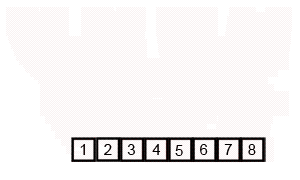
Сортировка слиянием пригодится для таких структур данных, в которых доступ к элементам осуществляется последовательно (например, для потоков). Здесь массив разбивается на две примерно равные части и каждая из них сортируется по отдельности. Затем два отсортированных подмассива сливаются в один.

Пирамидальная сортировка
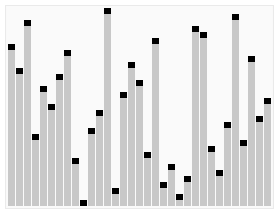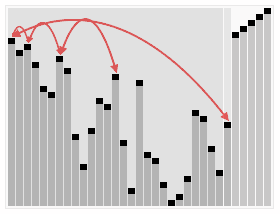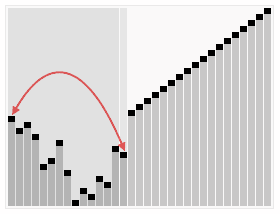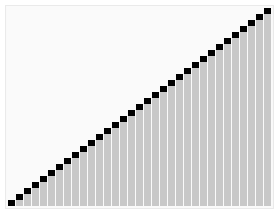
При этой сортировке сначала строится пирамида из элементов исходного массива. Пирамида (или двоичная куча) — это способ представления элементов, при котором от каждого узла может отходить не больше двух ответвлений. А значение в родительском узле должно быть больше значений в его двух дочерних узлах.
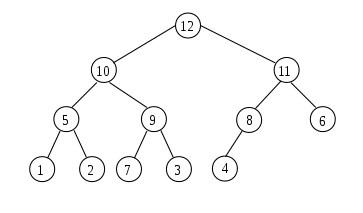
Пирамидальная сортировка похожа на сортировку выбором, где мы сначала ищем максимальный элемент, а затем помещаем его в конец. Дальше нужно рекурсивно повторять ту же операцию для оставшихся элементов.

