Стохастический Градиентный Спуск (SGD) имеет достаточно простую запись:
$$ x_{k+1} = x_k - \alpha_k g_k. $$
Здесь $g_k$ — это некоторая аппроксимация градиента целевой функции $\nabla f(x_k)$ в точке $x_k$, называемая стохастическим градиентом (или просто стох. градиентом), $\alpha_k > 0$ — это размер шага (stepsize, learning rate) на итерации $k$. Для простоты мы будем считать, что $\alpha_k = \alpha > 0$ для всех $k \geq 0$. Обычно предполагается, что стох. градиент является несмещённой оценкой $\nabla f(x_k)$ при фиксированном $x_k$: $\mathbb{E}\left(g_k \mid x_k\right) = \nabla f(x_k)$.
Доказательство сходимости
Зададимся следующим вопросом: с какой скоростью и в каком смысле SGD сходится к решению и сходится ли? Во-первых, как и во многих работах по стохастической оптимизации, нас будет интересовать сходимость метода в среднем, т.е. оценки на $\mathbb{E}\left(\vphantom{\frac14}\vert\vert x_k - x_\ast\vert\vert^2\right)$ или $\mathbb{E}\left(f(x_k) - f(x_\ast)\right)$, где $x_\ast$ — решение задачи (для простоты будем считать, что оно единственное).
Во-вторых, чтобы SGD сходился в указанном смысле, необходимо ввести дополнительные предположения. Действительно, например, если дисперсия стох. градиента не ограничена $\mathbb{E}\left(\vphantom{\frac14}\vert\vert g_k - \nabla f(x_k)\vert\vert^2 \mid x_k\right) = \infty$, то $\mathbb{E}\left(\vphantom{\frac14}\vert\vert x_k - x_\ast\vert\vert^2\right) = \infty$ и никаких разумных гарантий доказать не удаётся. Поэтому дополнительно к несмещённости часто предполагается, что дисперсия равномерно ограничена: предположим, что существует такое число $\sigma \ge 0$, что для всех $k \ge 0$ выполнено
$$ \mathbb{E}\left(\left.\vphantom{\frac14}\vert\vert g_k - \nabla f(x_k)\vert\vert^2\right| x_k\right) \leq \sigma^2. $$
Данное предположение выполнено, например, для задачи логистической регрессии (поскольку в данной задаче норма градиентов слагаемых ограничена), но в то же время является весьма обременительным. Его можно заменить на более реалистичные предположения, что мы немного затронем далее. Однако при данном предположении анализ SGD является очень простым и полезным для дальнейших обобщений и рассуждений.
Для простоты везде далее мы будем считать, что функция $f$ является $L$-гладкой и $\mu$-сильно выпуклой, т.е. для всех $x, y \in \mathbb{R}^d$ выполнены неравенства
$$ \vert\vert\nabla f(x) - \nabla f(y)\vert\vert \leq L\vert\vert x-y\vert\vert, $$
$$ f(y) \geq f(x) + \langle\nabla f(x), y- x \rangle + \frac{\mu}{2}\vert\vert y - x\vert\vert^2. $$
Теорема. Предположим, что $f$ является $L$-гладкой и $\mu$-сильно выпуклой, стох. градиент $g_k$ имеет ограниченную дисперсию, и размер шага удовлетворяет $0 < \alpha \leq 1/L$. Тогда для всех $k \geq 0$ выполняется неравенство
$$ \mathbb{E}\left(\vphantom{\frac14}\vert\vert x_k - x_{\ast}\vert\vert^2\right) \leq (1 - \alpha\mu)^k\vert\vert x_0 - x_{\ast}\vert\vert^2 + \frac{\alpha\sigma^2}{\mu}. $$
Доказательство. Используя выражение для $x_{k+1}$, мы выводим
$$ \vert\vert x_{k+1} - x_\ast \vert\vert^2 = \vert\vert x_k - x_{\ast} - \alpha g_k\vert\vert^2\ = \vert\vert x_k - x_{\ast}\vert\vert^2 - 2\alpha \langle x_k - x_{\ast}, g_k \rangle + \alpha^2 \vert\vert g_k\vert\vert^2 $$
Далее мы берём условное матожидание $\mathbb{E}\left(\cdot\mid x_k\right)$ от левой и правой частей и получаем:
$$ \mathbb{E}\left(\left.\vphantom{\frac14}\vert\vert x_{k+1} - x_\ast\vert\vert^2\right| x_k\right) = \vert\vert x_k - x_{\ast}\vert\vert^2 - 2\alpha\mathbb{E}\left( \langle x_k - x_{\ast}, g_k \rangle \mid x_k\right) + \alpha^2 \mathbb{E}\left(\left.\vphantom{\frac14}\vert\vert g_k\vert\vert^2\right| x_k\right)\ = \vert\vert x_k - x_{\ast}\vert\vert^2 - 2\alpha\left\langle x_k - x_{\ast}, \mathbb{E}\left(g_k \mid x_k\right) \right\rangle + \alpha^2 \mathbb{E}\left(\left.\vphantom{\frac14}\vert\vert g_k\vert\vert^2\right| x_k\right)\ = \vert\vert x_k - x_{\ast}\vert\vert^2 - 2\alpha\langle x_k - x_{\ast}, \nabla f(x_k)\rangle + \alpha^2 \mathbb{E}\left(\left.\vphantom{\frac14}\vert\vert g_k\vert\vert^2\right| x_k\right). $$
Следующий шаг в доказательстве состоит в оценке второго момента $\mathbb{E}\left(\vphantom{\frac14}\vert\vert g_k\vert\vert^2 \mid x_k\right)$. Используя предположение об ограниченности дисперсии стох. градиента, мы выводим:
$$ \mathbb{E}\left(\left.\vphantom{\frac14}\vert\vert g_k\vert\vert^2\right| x_k\right) = \mathbb{E}\left(\left.\vphantom{\frac14}\vert\vert\nabla f(x_k) + g_k - \nabla f(x_k)\vert\vert^2\right| x_k\right)\ = \vert\vert\nabla f(x_k)\vert\vert^2 + \mathbb{E}\left(\langle \nabla f(x_k), g_k - \nabla f(x_k) \rangle \mid x_k\right) + \mathbb{E}\left(\left.\vphantom{\frac14}\vert\vert g_k - \nabla f(x_k)\vert\vert^2 \right| x_k\right)\ = \vert\vert\nabla f(x_k)\vert\vert^2 + \left\langle \nabla f(x_k), \mathbb{E}\left(g_k - \nabla f(x_k) \mid x_k\right)\right\rangle + \mathbb{E}\left(\left.\vphantom{\frac14}\vert\vert g_k - \nabla f(x_k)\vert\vert^2 \right| x_k\right)\ = \vert\vert\nabla f(x_k)\vert\vert^2 + \mathbb{E}\left(\left.\vphantom{\frac14}\vert\vert g_k - \nabla f(x_k)\vert\vert^2 \right| x_k\right)\ \leq \vert\vert\nabla f(x_k)\vert\vert^2 + \sigma^2 $$
Чтобы оценить сверху $\vert\vert\nabla f(x_k)\vert\vert^2$, мы используем следующий факт, справедливый для любой выпуклой $L$-гладкой функции $f$ (см. книгу Ю. Е. Нестерова "Методы выпуклой оптимизации", 2010):
$$ \vert\vert\nabla f(x) - \nabla f(y)\vert\vert^2 \leq 2L\left(f(x) - f(y) - \langle \nabla f(y), x- y \rangle\right). $$
Беря в этом неравенстве $x = x_k$, $y = x_\ast$ и используя $\nabla f(x_\ast) = 0$, получаем
$$ \mathbb{E}\left(\left.\vphantom{\frac14}\vert\vert g_k\vert\vert^2\right| x_k\right) \leq 2L\left(f(x_k) - f(x_\ast)\right) + \sigma^2. $$
Далее мы подставляем эту оценку в выражение для $\mathbb{E}\left(\vert\vert x_{k+1} - x_\ast\vert\vert^2 \mid x_k\right)$:
$$ \mathbb{E}\left(\left.\vphantom{\frac14}\vert\vert x_{k+1} - x_\ast\vert\vert^2\right| x_k\right) \leq \vert\vert x_k - x_{\ast}\vert\vert^2 - 2\alpha\langle x_k - x_{\ast}, \nabla f(x_k)\rangle + 2\alpha^2L\left(f(x_k) - f(x_\ast)\right) + \alpha^2\sigma^2. $$
Остаётся оценить скалярное произведение в правой части неравенства. Это можно сделать, воспользовавшись сильной выпуклостью функции $f$: из
$$ f(x_\ast) \geq f(x_k) + \langle\nabla f(x_k), x_\ast - x_k \rangle + \frac{\mu}{2}\vert\vert x_\ast - x_k\vert\vert^2 $$
следует
$$ \langle\nabla f(x_k), x_k - x_\ast \rangle \geq f(x_k) - f(x_\ast) + \frac{\mu}{2}\vert\vert x_k - x_\ast\vert\vert^2. $$
Используя это неравенство в выведенной ранее верхней оценке на $\mathbb{E}\left(\vert\vert x_{k+1} - x_\ast\vert\vert^2\mid x_k\right)$, мы приходим к следующему неравенству:
$$ \mathbb{E}\left(\left.\vphantom{\frac14}\vert\vert x_{k+1} - x_\ast\vert\vert^2\right| x_k\right) \leq (1-\alpha\mu)\vert\vert x_k - x_{\ast}\vert\vert^2 -2\alpha(1 - \alpha L)\left(f(x_k) - f(x_\ast)\right) + \alpha^2\sigma^2\ \leq (1-\alpha\mu)\vert\vert x_k - x_{\ast}\vert\vert^2 + \alpha^2\sigma^2, $$
где в последнем неравенстве мы воспользовались неотрицательностью $2\alpha(1 - \alpha L)\left(f(x_k) - f(x_\ast)\right)$, что следует из $0 < \alpha \leq 1/L$ и $f(x_k) \geq f(x_\ast)$. Чтобы получить результат, заявленный в теореме, нужно взять полное мат. ожидание от левой и правой частей полученного неравенства (воспользовавшись при этом крайне полезным свойством условного мат. ожидания — tower property: $\mathbb{E}\left(\mathbb{E}\left(\cdot\mid x^k\right)\right) = \mathbb{E}\left(\cdot\right)$)
$$ \mathbb{E}\left(\vphantom{\frac14}\vert\vert x_{k+1} - x_\ast\vert\vert^2\right) \leq (1-\alpha\mu)\mathbb{E}\left(\vphantom{\frac14}\vert\vert x_k - x_{\ast}\vert\vert^2\right) + \alpha^2\sigma^2, $$
а затем, применяя это неравенство для $\mathbb{E}\left(\vphantom{\frac14}\vert\vert x_k - x_{\ast}\vert\vert^2\right)$, $\mathbb{E}\left(\vphantom{\frac14}\vert\vert x_{k-1} - x_{\ast}\vert\vert^2\right)$, $\ldots$ , $\mathbb{E}\left(\vphantom{\frac14}\vert\vert x_1 - x_{\ast}\vert\vert^2\right)$, получим
$$ \mathbb{E}\left(\vphantom{\frac14}\vert\vert x_{k+1} - x_\ast\vert\vert^2\right) \leq (1-\alpha\mu)^{k+1}\vert\vert x_0 - x_{\ast}\vert\vert^2 + \alpha^2\sigma^2\sum\limits_{t=0}^k (1-\alpha\mu)^t\ \leq (1-\alpha\mu)^{k+1}\vert\vert x_0 - x_{\ast}\vert\vert^2 + \alpha^2\sigma^2\sum\limits_{t=0}^\infty (1-\alpha\mu)^t\ = (1 - \alpha\mu)^{k+1}\vert\vert x_0 - x_{\ast}\vert\vert^2 + \frac{\alpha\sigma^2}{\mu}, $$
что и требовалось доказать.
Данный результат утверждает, что SGD с потоянным шагом сходится линейно к окрестности решения, радиус которой пропорционален $\tfrac{\sqrt{\alpha} \sigma}{\sqrt{\mu}}$. Отметим, что чем больше размер шага $\alpha$, тем быстрее SGD достигает некоторой окрестности решения, в которой продолжает осциллировать. Однако чем больше размер шага, тем больше эта окрестность. Соответственно, чтобы найти более точное решение, необходимо уменьшать размер шага в SGD. Этот феномен хорошо проиллюстрирован здесь.
Теорема выше доказана при достаточно обременительных предположениях: мы предположили, что функция является сильно выпуклой, $L$-гладкой и стох. градиент имеет равномерно ограниченную дисперсию. В практически интересных задачах данные условия (в данном виде) выполняются крайне редко. Тем не менее, выводы, которые мы сделали из доказанной теоремы, справедливы для многих задач, не удовлетворяющих введённым предположениям (во многом потому, что указанные свойства важны лишь на некотором компакте вокруг решения задачи, что в свою очередь не так и обременительно).
Более того, если мы сделаем немного другое предположение о стохастических градиентах, то сможем покрыть некоторые случаи, когда дисперсия не является равномерно ограниченной на всём пространстве. Предположим теперь, что $g_k = \nabla f_{\xi_k}(x_k)$, где $\xi_k$ просэмплировано из некоторого распределения $\cal D$ независимо от предыдущих итераций, $f(x) = \mathbb{E}_{\xi\sim \cal D}\left(f_{\xi}(x)\right)$ и $f_{\xi}(x)$ является выпуклой и $L_{\xi}$-гладкой для всех $\xi$ (данное предположение тоже можно ослабить, но для простоты изложения остановимся именно на такой формулировке). Будем называть данные условия предположением о выпуклых гладких стохастчиеских реализациях. Они выполнены, например, для задач линейно регрессии и логистической регрессии.
В таком случае, для точек, сгенерированных SGD, справедливо, что SGD с потоянным шагом сходится линейно к окрестности решения, радиус которой пропорционален $\tfrac{\sqrt{\alpha} \sigma}{\sqrt{\mu}}$. Отметим, что чем больше размер шага $\alpha$, тем быстрее SGD достигает некоторой окрестности решения, в которой продолжает осциллировать. Однако чем больше размер шага, тем больше эта окрестность. Соответственно, чтобы найти более точное решение, необходимо уменьшать размер шага в SGD. Этот феномен хорошо проиллюстрирован здесь.
Теорема выше доказана при достаточно обременительных предположениях: мы предположили, что функция является сильно выпуклой, $L$-гладкой и стох. градиент имеет равномерно ограниченную дисперсию. В практически интересных задачах данные условия (в данном виде) выполняются крайне редко. Тем не менее, выводы, которые мы сделали из доказанной теоремы, справедливы для многих задач, не удовлетворяющих введённым предположениям (во многом потому, что указанные свойства важны лишь на некотором компакте вокруг решения задачи, что в свою очередь не так и обременительно).
Более того, если мы сделаем немного другое предположение о стохастических градиентах, то сможем покрыть некоторые случаи, когда дисперсия не является равномерно ограниченной на всём пространстве. Предположим теперь, что $g_k = \nabla f_{\xi_k}(x_k)$, где $\xi_k$ просэмплировано из некоторого распределения $\cal D$ независимо от предыдущих итераций, $f(x) = \mathbb{E}_{\xi\sim \cal D}\left(f_{\xi}(x)\right)$ и $f_{\xi}(x)$ является выпуклой и $L_{\xi}$-гладкой для всех $\xi$ (данное предположение тоже можно ослабить, но для простоты изложения остановимся именно на такой формулировке). Будем называть данные условия предположением о выпуклых гладких стохастчиеских реализациях. Они выполнены, например, для задач линейно регрессии и логистической регрессии.
В таком случае, для точек, сгенерированных SGD, справедлив следующий результат.
Теорема. Предположим, что $f$ является $L$-гладкой и $\mu$-сильно выпуклой, стохастчиеские реализации являются выпуклыми и гладкими, и размер шага удовлетворяет $0 < \alpha \leq 1/2L_{\max}$, где $L_{\max} = \max_{\xi\sim \cal D} L_{\xi}$. Тогда для всех $k \geq 0$ выполняется неравенство
$$ \mathbb{E}\left(\vphantom{\frac14}\vert\vert x_k - x_{\ast}\vert\vert^2\right) \leq (1 - \alpha\mu)^k\vert\vert x_0 - x_{\ast}\vert\vert^2 + \frac{2\alpha\sigma_\ast^2}{\mu}, $$
где $\sigma_\ast^2 = \mathbb{E}_{\xi\sim \cal D}\vert\vert\nabla f_{\xi}(x_\ast)\vert\vert^2$.
Доказательство. Аналогично предыдущей доказательству предыдущей теоремы, получаем
$$ \mathbb{E}\left(\left.\vphantom{\frac14}\vert\vert x_{k+1} - x_\ast\vert\vert^2\right| x_k\right) = \vert\vert x_k - x_{\ast}\vert\vert^2 - 2\alpha\langle x_k - x_{\ast}, \nabla f(x_k)\rangle + \alpha^2 \mathbb{E}\left(\left.\vphantom{\frac14}\vert\vert g_k\vert\vert^2\right| x_k\right). $$
Поскольку $f_{\xi}(x)$ является выпуклой и $L_\xi$-гладкой, имеем (см. книгу Ю. Е. Нестерова "Методы выпуклой оптимизации", 2010):
$$ \vert\vert\nabla f_{\xi}(x) - \nabla f_{\xi}(y)\vert\vert^2 \leq 2L_{\xi}\left(f_{\xi}(x) - f_{\xi}(y) - \langle \nabla f_{\xi}(y), x - y \rangle\right). $$
Применяя это неравенство для $x = x_k$, $y = x_{\ast}$, получаем
$$ \mathbb{E}\left(\left.\vphantom{\frac14}\vert\vert g_k\vert\vert^2\right| x_k\right) = \mathbb{E}_{\xi_k \sim \mathcal{D}}\left(\vert\vert\nabla f_{\xi_k}(x_k) - \nabla f_{\xi_k}(x_\ast) + \nabla f_{\xi_k}(x_\ast)\vert\vert^2\right)\\ \leq 2\mathbb{E}_{\xi_k \sim \mathcal{D}}\left(\vert\vert\nabla f_{\xi_k}(x_k) - \nabla f_{\xi_k}(x_\ast)\vert\vert^2\right) + 2\mathbb{E}_{\xi_k \sim \mathcal{D}}\left(\vert\vert\nabla f_{\xi_k}(x_\ast)\vert\vert^2\right)\\ \leq \mathbb{E}_{\xi_k \sim \mathcal{D}}\left(4L_{\xi_k}\left(f_{\xi_k}(x_k) - f_{\xi_k}(x_\ast) - \langle \nabla f_{\xi_k}(x_\ast), x_k - x_\ast \rangle\right)\right) + 2\mathbb{E}_{\xi \sim \mathcal{D}}\left(\vert\vert\nabla f_{\xi_k}(x_\ast)\vert\vert^2\right)\\ \leq 4L_{\max} \left(f(x_k) - f(x_\ast) - \langle \nabla f(x_\ast), x_k - x_\ast\rangle\right) + 2\sigma_{\ast}^2 \\ = 4L_{\max} \left(f(x_k) - f(x_\ast)\right) + 2\sigma_{\ast}^2, $$
где во втором переходе мы воспользовались стандартным фактом: $\vert\vert a+b\vert\vert^2 \leq \vert\vert a\vert\vert^2 + \vert\vert b\vert\vert^2$ для любых $a, b \in \mathbb{R}^n$. Подставим полученное неравенство в выражение для $\mathbb{E}\left(\vert\vert x_{k+1} - x_\ast\vert\vert^2 \mid x_k\right)$, доказанное ранее:
$$ \mathbb{E}\left(\left.\vphantom{\frac14}\vert\vert x_{k+1} - x_\ast\vert\vert^2\right| x_k\right) = \vert\vert x_k - x_{\ast}\vert\vert^2 - 2\alpha\langle x_k - x_{\ast}, \nabla f(x_k)\rangle + 4L_{\max}\alpha^2 \left(f(x_k) - f(x_\ast)\right) + 2\alpha^2\sigma_{\ast}^2. $$
Остаётся оценить скалярное произведение в правой части неравенства. Это можно сделать, воспользовавшись сильной выпуклостью функции $f$: из
$$ f(x_\ast) \geq f(x_k) + \langle\nabla f(x_k), x_\ast - x_k \rangle + \frac{\mu}{2}\vert\vert x_\ast - x_k\vert\vert^2 $$
следует
$$ \langle\nabla f(x_k), x_k - x_\ast \rangle \geq f(x_k) - f(x_\ast) + \frac{\mu}{2}\vert\vert x_k - x_\ast\vert\vert^2. $$
Используя это неравенство в выведенной ранее верхней оценке на $\mathbb{E}\left(\vert\vert x_{k+1} - x_\ast\vert\vert^2 \mid x_k\right)$, мы приходим к следующему неравенству:
$$ \mathbb{E}\left(\left.\vphantom{\frac14}\vert\vert x_{k+1} - x_\ast\vert\vert^2\right| x_k\right) \leq (1-\alpha\mu)\vert\vert x_k - x_{\ast}\vert\vert^2 -2\alpha(1 - 2\alpha L_{\max})\left(f(x_k) - f(x_\ast)\right) + 2\alpha^2\sigma^2\ \leq (1-\alpha\mu)\vert\vert x_k - x_{\ast}\vert\vert^2 + 2\alpha^2\sigma_{\ast}^2, $$
где в последнем неравенстве мы воспользовались неотрицательностью $2\alpha(1 - 2\alpha L_{\max})\left(f(x_k) - f(x_\ast)\right)$, что следует из $0 < \alpha \leq 1/2L_{\max}$ и $f(x_k) \geq f(x_\ast)$. Действуя по аналогии с доказательством предыдущей теоремы, получаем требуемый результат.
Выводы, которые можно сделать из данной теоремы, очень похожи на те, что мы уже сделали из прошлой теоремы. Главные отличия заключаются в том, что $L_{\max}$ может быть гораздо больше $L$, т.е. максимальный допустимый размер шага $\alpha$ в данной теореме может быть гораздо меньше, чем в предыдущей. Однако размер окрестности теперь зависит от дисперсии стох. градиента в решении $\sigma_\ast^2$, что может быть значительно меньше $\sigma^2$.
Рассмотрим важный частный случай — задачи минимизации суммы функций:
$$ \min\limits_{x \in \mathbb{R}^d}\left\{f(x) = \frac{1}{n}\sum\limits_{i=1}^n f_i(x)\right\}. $$
Обычно $f_i(x)$ имеет смысл функции потерь на $i$-м объекте датасета. Предположим, что $f_i(x)$ — выпуклая и $L_i$-гладкая функция. Тогда выполняется предположение о выпуклых гладких стохастчиеских реализациях: действительно, достаточно задать $\xi$ как случайное число из ${1,2,\ldots,n}$, имеющее равномерное распределение. Тогда справедлив результат предыдущей теоремы с $L_{\max} = \max_{i\in 1,\ldots,n)}L_i$ и $\sigma_\ast^2 = \tfrac{1}{n}\sum_{i=1}^n \vert\vert\nabla f_i(x_\ast)\vert\vert^2$.
Для любого $K \ge 0$ можно выбрать шаг в SGD следующим образом:
$$ \text{если } K \leq \frac{2L_{\max}}{\mu}, \gamma_k = \frac{1}{2L_{\max}},\ \text{если } K > \frac{2L_{\max}}{\mu} \text{ и } k < k_0, \gamma_k = \frac{1}{2L_{\max}},\ \text{если } K > \frac{2L_{\max}}{\mu} \text{ и } k \geq k_0, \gamma_k = \frac{1}{4L_{\max} + \mu(k-k_0)}, $$
где $k_0 = \lceil K/2 \rceil$. Тогда из доказанного выше результата следует (см. Лемму 3 из статьи С. Стиха), что после $K$ итераций
$$ \mathbb{E}\left(\vphantom{\frac14}\vert\vert x_K - x_\ast\vert\vert^2\right) = \cal O\left(\frac{L_{\max} \vert\vert x_0 - x_\ast\vert\vert^2}{\mu}\exp\left(-\frac{\mu}{L_{\max}}K\right) + \frac{\sigma_{\ast}^2}{\mu^2 K}\right). $$
Таким образом, чтобы гарантировать $\mathbb{E}\left(\vphantom{\frac14}\vert\vert x_K - x_\ast\vert\vert^2\right) \leq \varepsilon$, SGD требуется
$$ \cal O\left(\frac{L_{\max} }{\mu}\log\left(\frac{L_{\max} \vert\vert x_0 - x_\ast\vert\vert^2}{\mu\varepsilon}\right) + \frac{\sigma_{\ast}^2}{\mu^2 \varepsilon}\right) $$
итераций/подсчётов градиентов слагаемых. Чтобы гарантировать то же самое, градиентному спуску (GD) необходимо сделать
$$ \cal O\left(n\frac{L}{\mu}\log\left(\frac{\vert\vert x_0 - x_\ast\vert\vert^2}{\varepsilon}\right)\right) $$
подсчётов градиентов слагаемых, поскольку каждая итерация GD требует $n$ подсчётов градиентов слагаемых (нужно вычислять полный градиент $\nabla f(x) = \tfrac{1}{n}\sum_{i=1}^n \nabla f_i(x)$). Можно показать, что $L \leq L_{\max} \leq nL$, поэтому в худшем случае полученная оценка для SGD заведомо хуже, чем для GD. Однако в случае, когда $L_{\max} = \cal O(L)$, однозначного вывода сделать нельзя: при большом $\varepsilon$ может доминировать первое слагаемое в оценке сложности SGD, поэтому в таком случае SGD будет доказуемо быстрее, чем GD (если пренебречь логарифмическими множителями).
Иными словами, чтобы достичь не очень большой точности решения, выгоднее использовать SGD, чем GD. В ряде ситуаций небольшой точности вполне достаточно, но так происходит не всегда. Поэтому возникает ествественный вопрос: можно ли так модифицировать SGD, чтобы полученный метод сходился линейно асимптотически к точному решению (а не к окрестности как SGD), но при этом стоимость его итераций была сопоставима со стоимостью итераций SGD? Оказывается, что да и соответствующие методы называются методами редукции дисперсии.
Методы редукции дисперсии
Перед тем, как мы начнём говорить о методах редукции дисперсии, хотелось бы раскрыть подробнее причину того, что SGD не сходится линейно асимптотически к точному решению. Мы рассмотрели анализ SGD в двух предположениях, и в обоих случаях нам требовалось вывести некоторую верхнюю оценку на второй момент стох. градиента, т.е. на $\mathbb{E}\left(\vert\vert g_k\vert\vert^2 \mid x_k\right)$. В обоих случаях эта оценка содержала некоторый константный член ($\sigma^2$ или $2\sigma_\ast^2$ — зависит от рассматриваемого предположения), который потом возникал и в финальной оценке на $\mathbb{E}\left(\vphantom{\frac14}\vert\vert x_k - x_\ast\vert\vert^2\right)$, препятствуя тем самым линейно сходимости метода. Конечно, это рассуждение существенно опирается на конкретный способ анализа метода, а потому не является строгим объяснением, почему SGD не сходится линейно.
Однако важно отметить, что оценка на $\mathbb{E}\left(\vert\vert g_k\vert\vert^2 \mid x_k\right)$ достаточно точно отражает поведение метода вблизи решения: даше если точка $x_k$ оказалась по какой-то причине близка к решению $x_\ast$ (или даже просто совпала с решением), то $\mathbb{E}\left(\vert\vert g_k\vert\vert^2 \mid x_k\right)$ и, в частности, $\mathbb{E}\left(\vert\vert g_k - \nabla f(x_k)\vert\vert^2 \mid x_k\right)$ будут порядка $\sigma^2$ или $\sigma_{\ast}^2$. Следовательно, при следующем шаге метод с большой вероятностью отдалится от/выйдет из решения, поскольку $\mathbb{E}\left(\vphantom{\frac14}\vert\vert x_{k+1} - x_k\vert\vert^2\right) = \alpha^2\mathbb{E}\left(\vphantom{\frac14}\vert\vert g_k\vert\vert^2\right) \sim \alpha^2\sigma^2$ или $\alpha^2\sigma_{\ast}^2$.
Из приведённых выше рассуждений видно, что дисперсия стох. градиента мешает методу сходится линейно к точному решению. Поэтому хотелось бы как-то поменять правило вычисления стох. градиента, чтобы выполнялись 3 важных свойства: (1) новый стох. градиент должен быть не сильно дороже в плане вычислений, чем подсчёт стох. градиента в SGD (градиента слагаемого), (2) новый стох. градиент должен быть несмещённой оценкой полного градиента $\nabla f(x_k)$, и (3) дисперсия нового стох. градиента должна уменьшаться в процессе работы метода. Например, можно рассмотреть следующий стох. градиент:
$$ g_k = \nabla f_{j_k}(x_k) + s_k, $$
где $j_k$ выбирается случайно равновероятно из множества ${1, 2, \ldots, n}$ и $\mathbb{E}\left(s_k\mid x_k\right) = 0$. В таком случае, будет выполнено свойство (2) из списка выше. Чтобы достичь желаемой цели, необходимо как-то специфицировать выбор случайного вектора $s_k$. Исторически одним из первых способов выбора $s_k$ был $s_k = -\nabla f_{j_k}(w_k) + \nabla f(w_k)$, где точка $w_k$ обновляется раз в $m \sim n$ итераций:
$$ w_{k+1} = \begin{cases} w_k, & \text{if } k+1 \mod m \neq 0,\ x_{k+1}, & \text{if } k+1 \mod m = 0. \end{cases} $$
Данный метод называется Stochastic Variance Reduced Gradient (SVRG). Данный методы был предложен и проанализирован в NeurIPS статье Джонсона и Жанга в 2013 году. Теперь же убедимся, что метод удовлетворяет всем трём отмеченным свойствам. Начнём с несмещённости:
$$ g_k = \nabla f_{j_k}(x_k) - \nabla f_{j_k}(w_k) + \nabla f(w_k), $$
$$ \mathbb{E}\left(g_k\mid x_k\right) = \frac{1}{n}\sum\limits_{i=1}^n \left(\nabla f_{i}(x_k) - \nabla f_{i}(w_k) + \nabla f(w_k)\right) = \nabla f(x_k). $$
Далее, вычисление $g_k$ подразумевает 2 подсчёта градентов слагаемых при $k \mod m \neq 0$ и $n+2$ подсчёта градентов слагаемых при $k \mod m \neq 0$. Таким образом, за $m$ последователльных итераций SVRG происходит вычисление $2(m-1) + n + 2 = 2m + n$ градиентов слагаемых, в то время как SGD требуется $m$ подсчётов градиентов слагаемых. Если $m = n$ (стандартный выбор параметра $m$), то $n$ итераций SVRG лишь в 3 раза дороже, чем $n$ итераций SGD. Иными словами, в среднем итерация SVRG не сильно дороже итерации SGD.
Наконец, если мы предположим, что метод сходится $\mathbb{E}\left(\vphantom{\frac14}\vert\vert x_k - x_\ast\vert\vert^2\right) \to 0$ (а он действительно сходится, см., например, доказательство вот тут), то получим, что $\mathbb{E}\left(\vphantom{\frac14}\vert\vert w_k - x_\ast\vert\vert^2\right) \to 0$, а значит $\mathbb{E}\left(\vphantom{\frac14}\vert\vert x_k - w_k\vert\vert^2\right) \to 0$ и $\mathbb{E}\left(\vphantom{\frac14}\vert\vert\nabla f(w_k)\vert\vert^2\right) \to 0$. Но тогда в силу Липшицевости градиентов $f_i$ для всех $i=1,\ldots,n$ имеем:
$$ \mathbb{E}\left(\vphantom{\frac14}\vert\vert g_k\vert\vert^2\right) = \mathbb{E}\left(\vphantom{\frac14}\vert\vert\nabla f_{j_k}(x_k) - \nabla f_{j_k}(w_k) + \nabla f(w_k)\vert\vert^2\right)\ \leq 2\mathbb{E}\left(\vphantom{\frac14}\vert\vert\nabla f_{j_k}(x_k) - \nabla f_{j_k}(w_k)\vert\vert^2\right) + 2\mathbb{E}\left(\vphantom{\frac14}\vert\vert\nabla f(w_k)\vert\vert^2\right)\ \leq 2L_{\max} \mathbb{E}\left(\vphantom{\frac14}\vert\vert x_k - w_k\vert\vert^2\right) + 2\mathbb{E}\left(\vphantom{\frac14}\vert\vert\nabla f(w_k)\vert\vert^2\right) \to 0, $$
а значит, дисперсия $g_k$ стремится к нулю.
Приведённые выше рассуждения не являются формальным доказательством сходимости метода, но частично объясняют, почему метод сходится и, самое главное, объясняют интуицию позади формул, задающих метод. Строгое доказательство можно прочитать вот тут. Мы же здесь приведём результат о сходимости немного другого метода — Loopless Stochastic Variance Reduced Gradient (L-SVRG), который был предложен в 2015 году и переоткрыт в 2019 году. Основное отличие от SVRG состоит в том, что точка $w_k$ теперь обновляется на каждой итерации с некоторой маленькой вероятностью $p \sim 1/n$:
$$ w_{k+1} = \begin{cases} w_k, & \text{с вероятностью } 1-p,\ x_{k}, & \text{с вероятностью } p. \end{cases} $$
Иными словами, L-SVRG имеет случайную длину цикла, в котором $w_k$ не обновляется. Вся интуиция и все наблюдения приведённые для SVRG выше, справедливы и для L-SVRG.
Можно доказать следующий результат.
Теорема. Предположим, что $f$ является $L$-гладкой, $\mu$-сильно выпуклой и имеет вид суммы, функции $f_i$ являются выпуклыми и $L_i$-гладкими для всех $i=1,\ldots, n$, и размер шага удовлетворяет $0 < \alpha \leq 1/6L_{\max}$, где $L_{\max} = \max_{i\in 1,\ldots,n} L_{i}$. Тогда для всех $k \geq 0$ для итераций L-SVRG выполняется неравенство
$$ \mathbb{E}\left(\vphantom{\frac14}\vert\vert x_k - x_{\ast}\vert\vert^2\right) \leq \left(1 - \min\left\{\alpha\mu, \frac{p}{2}\right\}\right)^kV_0, $$
где $V_0 = \vert\vert x_0 - x_\ast\vert\vert^2 + \tfrac{4\alpha^2}{p}\sigma_0^2$, $\sigma_0^2 = \tfrac{1}{n}\sum_{i=1}^n \vert\vert\nabla f_i(x_0) - \nabla f_i(x_\ast)\vert\vert$.
Замечание. В частности, если $\alpha = 1/6L_{\max}$ и $p = 1/n$, то
$$ \mathbb{E}\left(\vphantom{\frac14}\vert\vert x_k - x_{\ast}\vert\vert^2\right) \leq \left(1 - \min\left\{\frac{\mu}{6L_{\max}}, \frac{1}{2n}\right\}\right)^kV_0. $$
Следовательно, чтобы гарантировать $\mathbb{E}\left(\vphantom{\frac14}\vert\vert x_k - x_\ast\vert\vert^2\right) \leq \varepsilon$, L-SVRG требуется
$$ \cal O\left(\left(n + \frac{L_{\max} }{\mu}\right)\log\left(\frac{V_0}{\varepsilon}\right)\right) $$
итераций/подсчётов градиентов слагаемых (в среднем). Напомним, что чтобы гарантировать то же самое, градиентному спуску (GD) необходимо сделать
$$ \cal O\left(n\frac{L}{\mu}\log\left(\frac{L \vert\vert x_0 - x_\ast\vert\vert^2}{\mu\varepsilon}\right)\right) $$
подсчётов градиентов слагаемых, поскольку каждая итерация GD требует $n$ подсчётов градиентов слагаемых (нужно вычислять полный градиент $\nabla f(x) = \tfrac{1}{n}\sum_{i=1}^n \nabla f_i(x)$). Можно показать, что $L \leq L_{\max} \leq nL$, поэтому в худшем случае полученная оценка для L-SVRG не лучше, чем для GD. Однако в случае, когда $L_{\max} = \cal O(L)$, L-SVRG имеет сложность значительно лучше, чем GD (если пренебречь логарифмическими множителями).
В заключение этого раздела, хотелось бы отметить, что существуют и другие методы редукции дисперсии. Одним из самых популярных среди них является SAGA. В отличие от SVRG/L-SVRG, в методе SAGA хранится набор градиентов $\nabla f_1(w_k^1), \nabla f_2(w_k^2), \ldots, \nabla f_n(w_k^n)$. Здесь точка $w_k^i$ обозначает точку, в которой в последний раз был подсчитан градиент функции $i$ до итерации $k$. Формально это можно записать следующим образом:
$$ w_0^1 = w_0^2 = \ldots = w_0^n, $$
$$ g_k = \nabla f_{j_k}(x_k) - \nabla f_{j_k}(w_k^{j_k}) + \frac{1}{n}\sum\limits_{i=1}^n \nabla f_{i}(w_k^{i}), $$
$$ w_{k+1}^{j_k} = x_k, \quad w_{k+1}^i = w_k^i \text{ для всех } i \neq j_k, $$
$$ x_{k+1} = x_k - \alpha g_k. $$ Основное преимущество SAGA состоит в том, что не требуется вычислять полный градиент всей суммы по ходу работы метода, однако в начале требуется посчитать градиенты всех слагаемых (отмечаем здесь, что эта операция может быть гораздо дороже по времени, чем вычисление полного градиента) и, более того, требуется хранить $n$ векторов, что может быть недопустимо для больших датасетов. В плане теоретических гарантий SAGA и L-SVRG не отличимы.
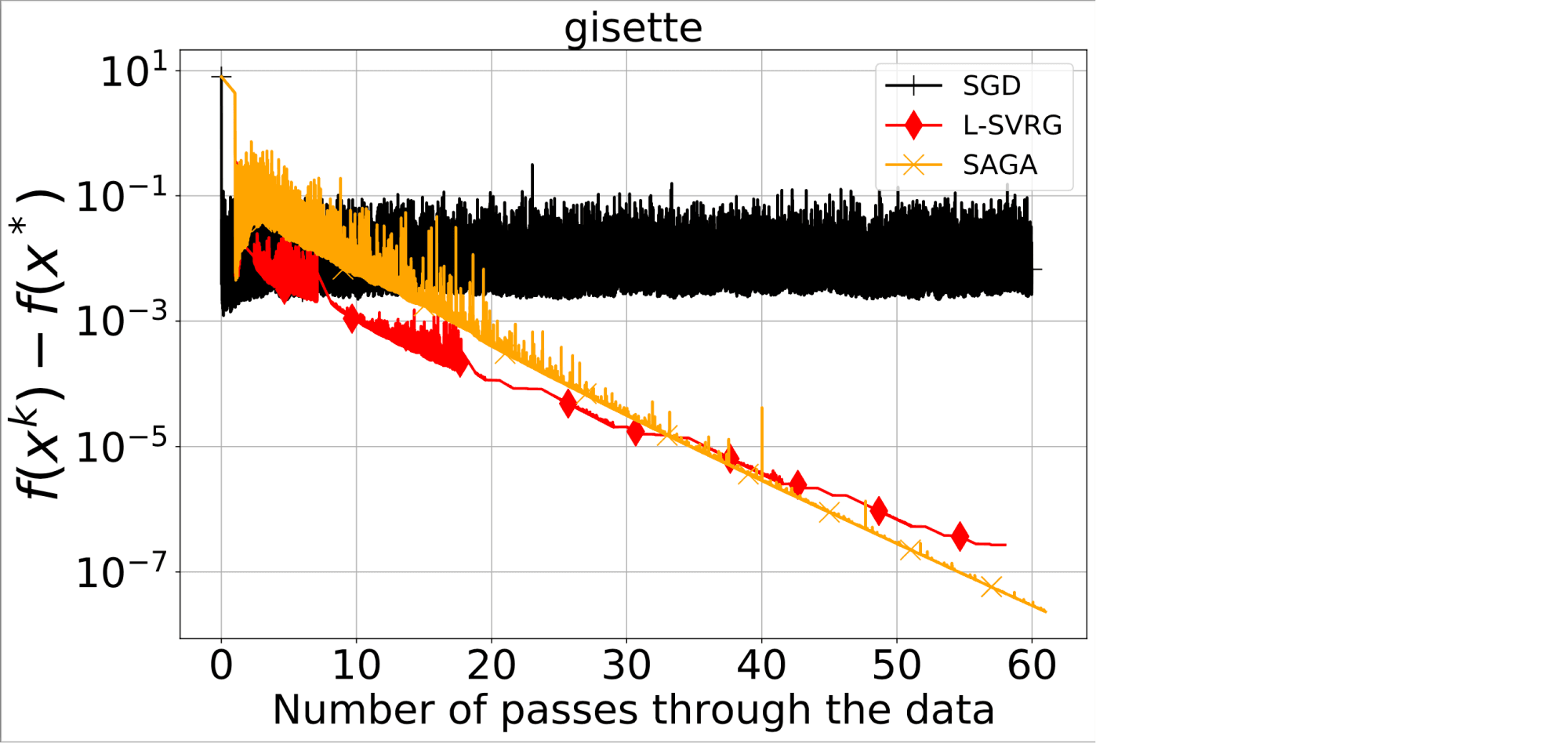
Ниже приведён график с траекториями SGD (с постоянным шагом), L-SVRG и SAGA при решении задачи логистической регрессии. Как можно видеть из графика, SGD достаточно быстро достигает не очень высокой точности и начинает осциллировать вокруг решения. В то же время, L-SVRG и SAGA достигают той же точности медленнее, но зато не осциллируют вокруг решения, а продолжают сходится (причём линейно).
Сравнение работы SGD, L-SVRG и SAGA при решении задачи логистической регрессии на датасете gisette из библиотеки LIBVSM.
