В этом разделе мы поговорим о том, как оптимизировать негладкие функции в ситуациях, когда «плохую» составляющую удаётся локализовать и она сравнительно несложная.
Проксимальная минимизация
Для того, чтобы подступиться к проксимальным методам, посмотрим на градиентный спуск с другой стороны. Для простоты рассмотрим константный размер шага $\alpha$. Перепишем шаг градиентного спуска следующим образом:
$$ \frac{x_{k+1} - x_k}{\alpha} = - \nabla f(x_k). $$
Посмотрим на это уравнение по-другому. Рассмотрим функцию $x(t)$, равную $x_k$ при $(k-1)\alpha < t \leq \alpha k$ ($t$ мы будем воспринимать, как некоторый временной параметр). Тогда при $t = \alpha k$:
$$ \frac{x(t + \alpha) - x(t)}{\alpha} = - \nabla f(x(t)). $$
Теперь слева не что иное, как аппроксимация производной! Если мы устремим $\alpha$ к нулю, то получится так называемое уравнение градиентного потока:
$$ \dot{x} = -\nabla f(x). $$
Эта динамика в случае выпуклой функции $f$ сходится к точке минимума $x^*$ из любой начальной точки при $t \to +\infty$. Сравнение между динамикой градиентного спуска и градиентного потока можно увидеть на следующем изображении:
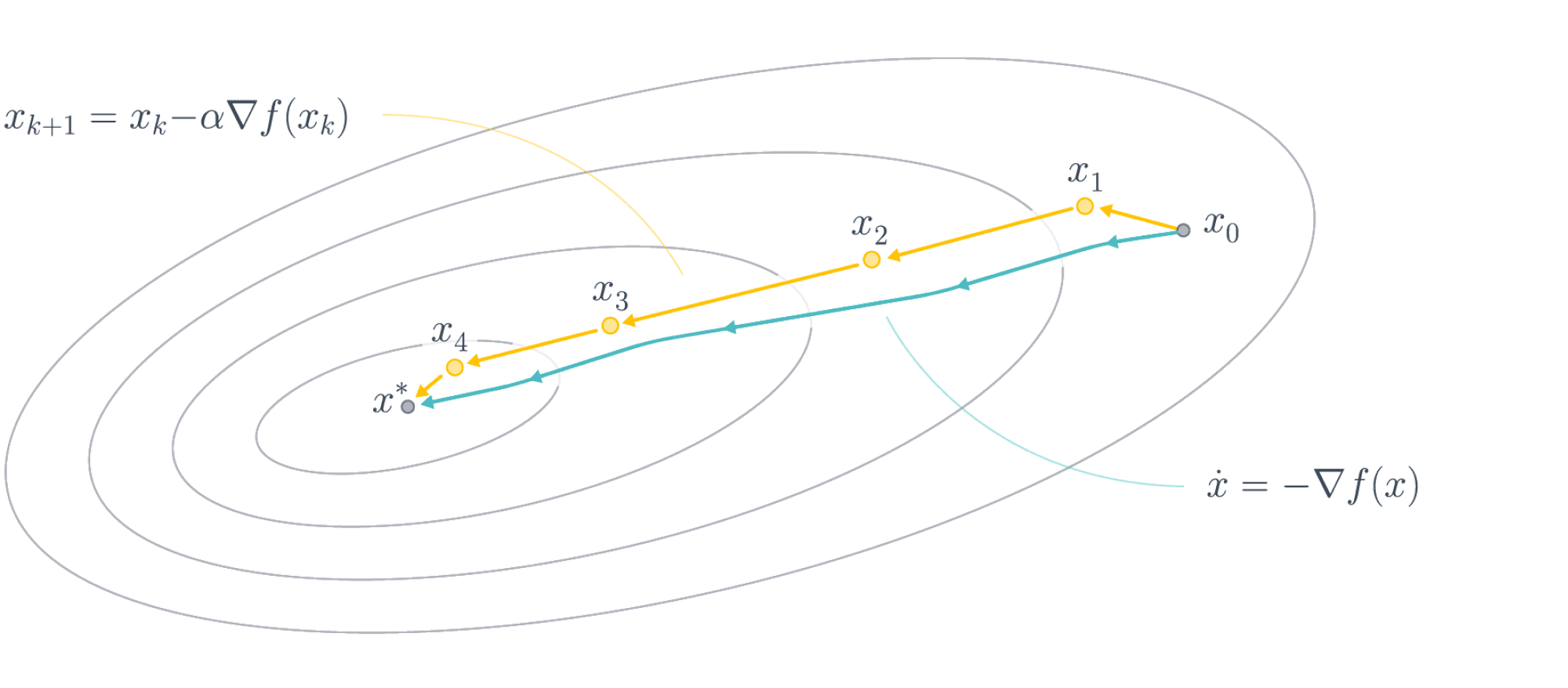
Первый состоит из дискретных шагов, второй же представляет из себя непрерывный процесс.
Нетрудно осознать физический смысл динамики $\dot{x} = -\nabla f(x)$: маленькое тело скатывается по склону графика функции так, что в любой момент её скорость совпадает с антиградиентом, то есть оно катится по направлению наискорейшего спуска.
Теперь представим, что мы сейчас занимается не машинным обучением, а численными методами. Перед нами есть обыкновенное дифференциальное уравнение (ОДУ), и его надо решить. Одним из численных методов решения ОДУ (более стабильным, чем обычная схема Эйлера) является обратная схема Эйлера (backward Euler scheme):
$$ \frac{x_{k+1} - x_k}{\alpha_k} = -\nabla f(x_{\color{red}{k+1}}). $$
В обратной схеме Эйлера мы делаем градиентный спуск, только градиент смотрим не в текущей точке (как было бы в обычной схеме Эйлера), а буквально в будущей. Занятная идея, только вот напрямую выразить $x_{k+1}$ из этого уравнения не получится. Нужно поступить чуть хитрее. Заметим, что
$$\frac{(x_{k+1} - x_k)_i}{\alpha_k} = \left.\frac{1}{2\alpha_k} (x - x_k)^2_i \right\vert_{x_{k+1}}$$
Это позволяет нам сказать, что весь вектор $\frac{x_{k+1} - x_k}{\alpha_k}$ является градиентом функции $g(u) = \frac{1}{2\alpha_k} \Vert u - x_{k} \Vert^2$, посчитанном в точке $x_{k+1}$. Тогда получаем, что $x_{k+1}$ удовлетворяет следующему условию:
$$ \nabla\left( g(u) + f(u) \right)(x_{k+1}) = 0. $$
Если функция $f(x)$ выпуклая, то $f(x) + g(x)$ тоже выпуклая, и её стационарная точка будет точкой минимума. Стало быть, $x_{k+1}$ можно высчитывать по формуле
$$ x_{k+1} = \arg\min_{u}\left\{ f(u) + \frac{1}{2\alpha_k}\Vert u - x_{k} \Vert^2 \right\}. $$
Определим прокс-оператор следующим образом:
$$ \mathrm{prox}_{f}(x) = \arg\min\left\{ f(u) + \frac{1}{2}\Vert u - x \Vert^2 \right\}. $$
Тогда, поскольку умножение на $\alpha_k > 0$ внутри арг-минимума не влияет на саму точку минимума, получаем следующую итеративную схему:
$$ x_{k+1} = \arg\min\left\{ \alpha_k \left(f(u) + \frac{1}{2\alpha_k}\Vert u - x \Vert^2 \right)\right\} = $$
$$ \arg\min\left\{ \alpha_k f(u) + \frac{1}{2}\Vert u - x \Vert^2 \right\}= \mathrm{prox}_{\alpha_k f}(x_k). $$
Итеративный процесс $x_{k+1} = \mathrm{prox}_{\alpha_k f}(x_k)$ называется методом проксимальной минимизации. Вы можете спросить себя: зачем он нужен? Ведь теперь на каждом шаге мы должны решать задачу оптимизации:
$$ \min_{u} f(u) + \frac{1}{2\alpha_k}\Vert u - x_k \Vert^2 $$
Если $f$ выпуклая, нам есть, что ответить: наличие второго слагаемого гарантирует сильную выпуклость задачи, то есть она решается достаточно эффективно. Но если $f$ не является выпуклой, то мы ничего не достигли этой модификацией.
Композитная оптимизация, проксимальный градиентный метод (PGM)
Чтобы понять, зачем нам понадобилась проксимальная оптимизация, рассмотрим оптимизацию функций вида
$$ \min_{x} { f(x) = g(x) + h(x)}, $$
где $g(x)$ – это гладкая функция, а $h(x)$ – это функция, для которой прокс-оператор считается аналитически. Воспользуемся следующим трюком: по $g$ мы совершим градиентный шаг, а по $h$ – проксимальный. Получаем следующую итеративную процедуру:
$$ x_{k+1} = \mathrm{prox}_{\alpha_k h} (x_k - \alpha_k \nabla g(x_k)); $$
Эта процедура определяет так называемый проксимальный градиентный метод (Proximal Gradient Method, PGM), который может использоваться, например, для решения задачи регрессии с $\ell_1$-регуляризацией.
ISTA (Iterative Shrinkage-Thresholding Algorithm)
Теперь решим конкретную задачу $\ell_1$-регрессии. Она выглядит следующим образом:
$$ \Vert y - Xw \Vert_2^2 + \lambda \Vert w \Vert_1 \to \min_w. $$
Мы хотим применить PGM к этой задаче, для этого нужно научиться вычислять прокс-оператор для $\ell_1$-нормы. Проделаем эту операцию:
$$ \mathrm{prox}_{\alpha \Vert \cdot \Vert_1}(x) = \arg\min_{u} \left\{ \Vert u \Vert_1 + \frac{1}{2 \alpha} \Vert u - x \Vert_2^2 \right\} = $$
$$ = \arg\min_{u} \left\{ \sum_{i=1}^d \vert u_i \vert + \frac{(u_i - x_i)^2}{2\alpha} \right\}. $$
Заметим, что каждое слагаемое зависит только от одной координаты. Это значит, что каждую координату мы можем прооптимизировать отдельно и получить $d$ одномерных задач минимизации вида
$$ \arg\min_{u_i} \left\{ \vert u_i \vert + \frac{(u_i - x_i)^2}{2\alpha} \right\}. $$
Решение такой одномерной задачи записывается в виде функции soft thresholding:
$$ \mathrm{prox}_{\alpha \Vert \cdot \Vert_1}(x)_i = \begin{cases} x_i - \alpha &, x_i \geq \alpha \ 0 & \vert x_i \vert \leq \alpha \ x_i + \alpha & x_i \leq - \alpha \end{cases} $$
Тогда мы получаем следующий алгоритм для $\ell_1$-регрессии, которые называется Iterative Shrinkage-Thresholding Algorithm (ISTA):
w = normal(0, 1) # инициализация
repeat S times: # другой вариант: while abs(err) > tolerance
f = X.dot(w) # посчитать предсказание
delta = f - y # посчитать отклонение предсказания
grad = 2 * X.T.dot(delta) / n # посчитать градиент
w_prime = w - alpha * grad # считаем веса, которые отправим в прокс
for i in range(d):
w[i] = soft_threshold(w_prime[i], alpha * llambda) # вычисляем прокс
Заметим одну крутую особенность этого алгоритма -- мы явно видим, что решение получается разреженное, ведь какие-то координаты будут явно зануляться при применении soft threshold! Причем чем больше размер и шага, и параметра регуляризации, тем больше прореживается координат.
Конкретно этот метод не применяется на практике, но используются его вариации. Например, статья, которая указана в главе про линейные модели о том, как работало предсказание CTR в google в 2012 году, также базируется на вычислении soft threshold как прокс-оператора.
Общие выводы
Подытожим все вышесказанное:
- Проксимальные методы – теоретически интересная идея для выпуклой оптимизации, которая должна давать более численно стабильные алгоритмы.
- Проксимальные методы позволяют достаточно эффективно решать задачи композитной оптимизации, в частности, $\ell_1$-регуляризованную задачу регрессии. Более того, используемые на практике решения задачи $\ell_1$-регуляризованной регрессии так или иначе базируются на идее ISTA.
- Также есть попытки использовать проксимальные методы для более сложных моделей. Например, статья о применении их в нейросетях.
Кроме того, есть имеются применения проксимальный методов для построения распределенных алгоритмов. Все подробности можно найти в монографии Neal Parikh и Stephen Boyd, мы же только привели применение этих идей в машинном обучении.